KV缓存系统改进方案
0.RPC通信
1.如何保证节点的一致性
1.涉及到两个节点中的数据同步操作。在增删改的时候需要同时对当前节点和下一个节点进行同时操作,如果一个成功一个不成功怎么办?
双方各存一个哈希表
把操作指令同时发送给当前节点和下一个节点,这两个指令不马上执行,而是放到,如果两边都收到指令,则返回true。这时候向两边同时发送commit信息,则把刚才的数据添加进表中。
2.如何手动停止一个存储节点?
通过获取这个节点的全局写锁,对节点进行删除操作。
2.如何提高中心节点的容灾性
待解决问题:
1. 中心节点性能瓶颈,以及容灾性问题
中心节点扩容问题,如何保证哈希环同步
2. 中心节点缓存同步问题
对缓存加锁,
中心节点哈希环分布不均匀问题
通过虚拟节点实现--如何在虚拟节点中找到下一个节点。
3.如何细粒度访问跳表
https://zhuanlan.zhihu.com/p/622177029
1.每个节点新增一个读写锁,写优先
2.在遍历过程中,for循环获取读锁,在修改/新增/删除的前一个节点,获取写锁。
3.get操作 -- 获取读锁
1.如何实现细粒度锁
1.1 应用场景
首先列举跳表两大工程应用场景,包括应用于 redis 中 zset 的实现,以及应用于 rocksdb 中 lsm tree 结构内存部分的数据结构实现.
由于 redis 采用单线程处理模型,因此不存在并发访问跳表的诉求;
rocksdb 则采用多线程处理模型,并发读写内存数据结构时,需要兼顾数据一致以及操作性能,此时就需要使用到并发安全的跳表结构.
与 rocksdb 类似,后续我们在基于跳表构建需要支持并发操作的有序表时,需要考虑应该采用何种并发模型进行实现.
1.2 全局读写锁
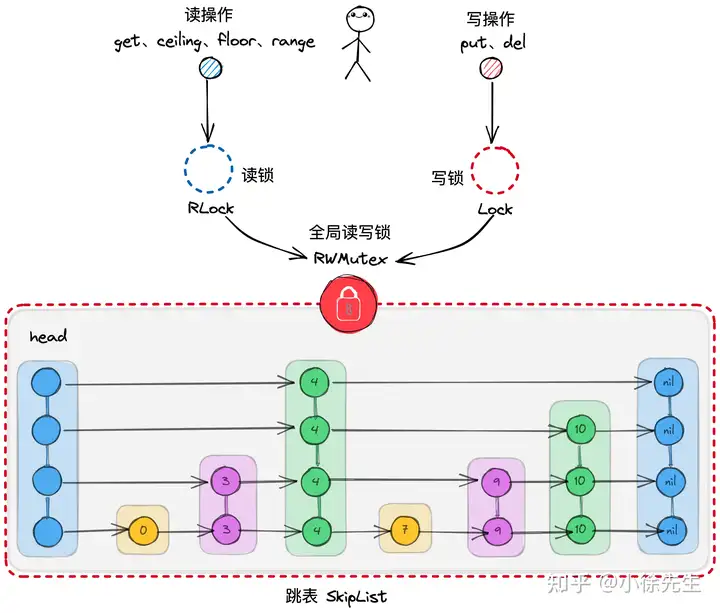
实现并发跳表最无脑的方式是,在基础跳表的基础之上,加上一把全局范围的读写锁. 所有写操作(put、del)需要持写锁保证写操作的独享性,所有读操作(get、ceiling、floor、range)等可以持读锁,保证读与读操作之间的共享性.
这种实现方式简单易懂,且可以很好地胜任于读多写少的使用场景,但由于其将并发写操作限制为串行化的执行模式,因此面对写多读少的场景,就会体现出一定的性能劣势.
在此基础上,我们回过头梳理并思考一个问题,对于跳表这种数据结构,在并发读写操作时,添加的锁粒度是否还有进一步细化的可能性,只要锁的范围变细,那么涉及到不同锁范围的写操作彼此之间是相互独立的,就可以在一定程度上提高数据结构的并发写性能.
1.3 细锁的可行性探讨
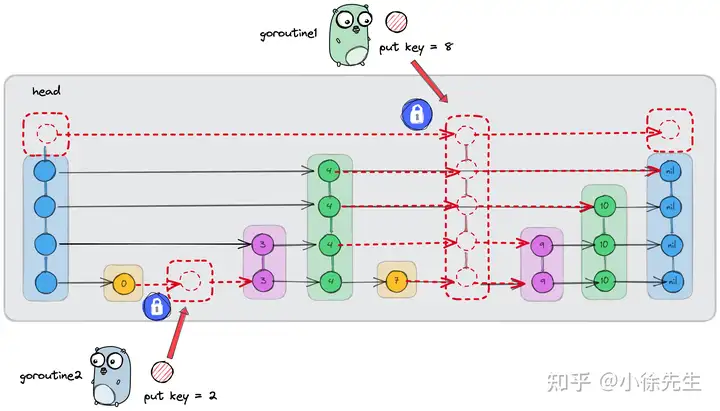
以一例具体的并发写 case 加以说明.
倘若在上图所示的跳表中,我们需要并发插入 {key : 2} 和 {key : 8} 的两个节点,其中 {key : 2} 节点的高度为 1,{key : 8} 节点的高度为 5,那么这两个操作是否可以不作互斥,并行处理呢?
答案是可以的.
跳表本身是基于一层层的单向链表构成. 在单向链表中,插入节点这件事情,本质上是通过调整拟插入位置前一个节点(后面统一称为左边界)的指针加以实现的. 以插入{key : 8} 为例,过程分为几步:
- 构造{key : 8}这个节点
- 令{key : 8}的next指向其左边界的next
- 令{key : 8}左边界的next指向{key : 8}
可以看出,对于链表而言,插入动作本身只涉及到对左边界的改动.
对于拟插入的 {key : 2} 而言,其左边界为:
- 第 0 层的 {key : 0};
对于拟插入的 {key : 8} 而言,其左边界为:
- 第 0 层的 {key : 7};
- 第 1、2、3 层的 {key : 4};
- 第 4 层的 head.
可以看出, {key : 2} 和 {key : 8} 的左边界是相互独立的. 因此,两笔插入操作哪怕是并发进行,彼此之间也不会产生干扰.
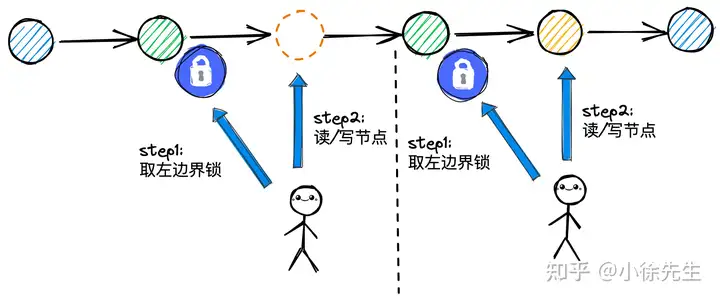
沿着这个思路出发,对于跳表的并发操作,其实可以尝试将锁的粒度由全局锁退化成节点锁,而这里所谓的节点指的是就是目标节点的左边界节点,对左边界节点上锁,意味着获得了其 next 指针所指向的下一个节点(或者该间隙范围)的操作所有权.
以下图中的单向链表为例,我们进一步对这种左边界锁模型加以示意,可以看到不管是插入、更新亦或是查询动作,左边界锁模型都是适用的.
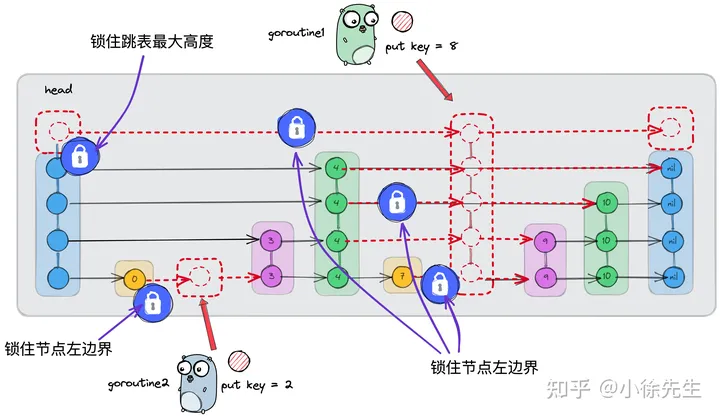
另一个需要加锁的位置在于跳表的最大高度. 在执行插入节点动作时,倘若新节点的高度超过了跳表现有的最大高度,则需要对跳表高度进行修改,这个过程涉及到对 head 的 nexts 数组进行扩容,我们需要保证其并发安全性. 因此我们规定规定,所有尝试修改跳表高度的插入操作,都必须在获得 head 的节点锁的基础之上串行进行.
综上所述,我们对跳表中的全局锁进行了细化,最终落到节点的维度,包含两部分:
- 对于拟操作的节点,需要逐层持有其左边界节点的节点锁
- 对于需要引起跳表高度变化的插入操作,需要持有头结点 head 的节点锁
2 落实到流程
下面以 1.3 小节的思路作为指导纲领,对跳表的几个核心方法进行流程梳理.
2.1 get
首先明确,跳表的 get 操作是适用于左边界锁模型.
get 操作的流程是从最高层的 head 节点出发,逐层遍历,直到找到 key 值小于 target 且最接近于 target 的左边界节点,然后再进行层数下降.
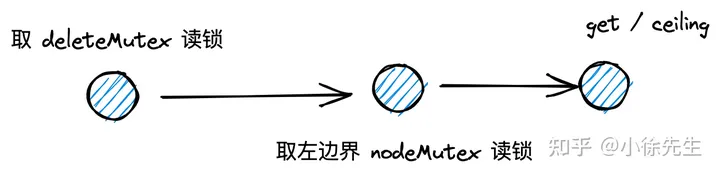
这整个过程和左边界锁模型高度契合,我们只需要对每层的左边界节点进行加锁(实际上可以加读锁,满足和其他的 get 操作共享),就能保证拟读取范围的并发安全性(通过左边界的读锁保护,实现了和相同范围内写操作的互斥).
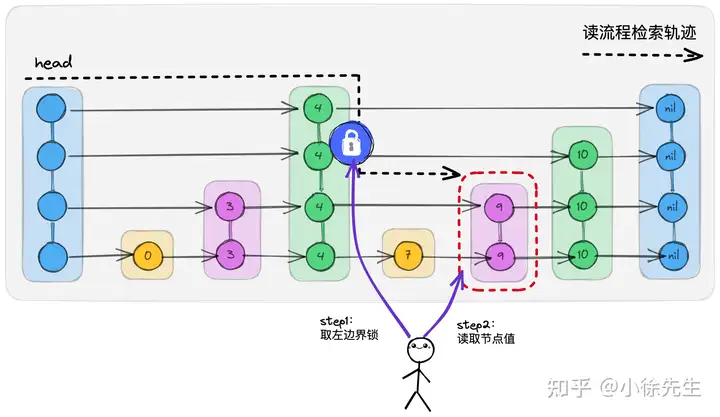
2.2 put
put 操作也是适用于左边界锁模型的.
首先,put 操作根据 key-value 对是否存在,还可以进一步拆分为更新和插入两种类型,因此在执行 put 的流程可以拆分为几步:
(1)检查 key-value 对是否存在
(2)如果 key-value 对存在,则直接对原节点进行值更新
(3)如果 key-value 对不存在,则需要插入新节点
(4)如果插入新节点的高度大于跳表当前高度,则需要进行高度扩容
为了保证上述(1)-(3)流程的原子性(避免对同一个 key 的并发写操作同时经过了第(2)步的校验,重复执行第(3)步动作),因此针对于相同 key 的 put 操作彼此之前是需要互斥的,需要通过一把 key 锁进行约束保护.
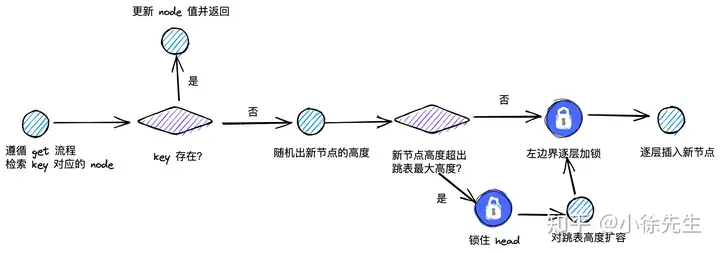
put 操作的整体流程如上图所示:
- 针对于同一个 key 的 put 操作需要互斥
- 在上述第(1)步中,采用类似于 get 流程的方式,逐层对左边界节点加读锁,直到获取到目标 node 或者遍历结束为止;
- 倘若 node 存在,代表这是更新操作,则直接更新节点值即可;
- 倘若 node 不存在,则需要构造一个新节点 newNode,并且随机出新节点的最大高度
- 倘若 newNode 最大高度大于跳表当前高度,则需要对 head 加锁,然后进行高度扩容
- 接下来沿 head 从 newNode 高度对应的层数出发,逐层遍历,直到来到左边界
- 逐层对左边界节点加写锁,以实现和 get 操作中相同范围数据的互斥
- 逐层插入新节点
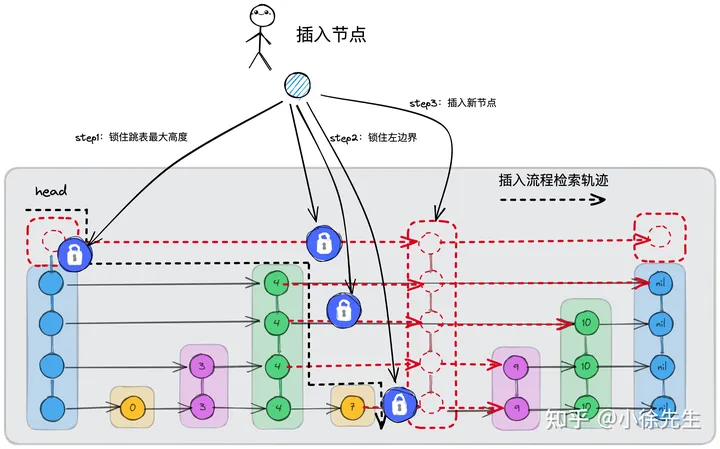
2.3 delete
删除操作具有特殊性,它的存在可能会导致左边界锁模型的失效,因此删除操作需要和 get、put 操作互斥,单独串行处理.
由于跳表通过一系列单向链表组成,因此删除操作只需要调整左边界的指针引用,就可以绕开被删除节点本身,直接实现节点的删除效果.
换言之,这种删除操作可以令得其他 goroutine 在拟删除节点上加的锁无效化. 在这样的设定之下,当我们基于 get 或者 put 操作来到某层左边界位置并且持有左边界锁时,也不一定能保证自身的合法性,因为这把锁可能因为左边界节点被删除而产生无效化.
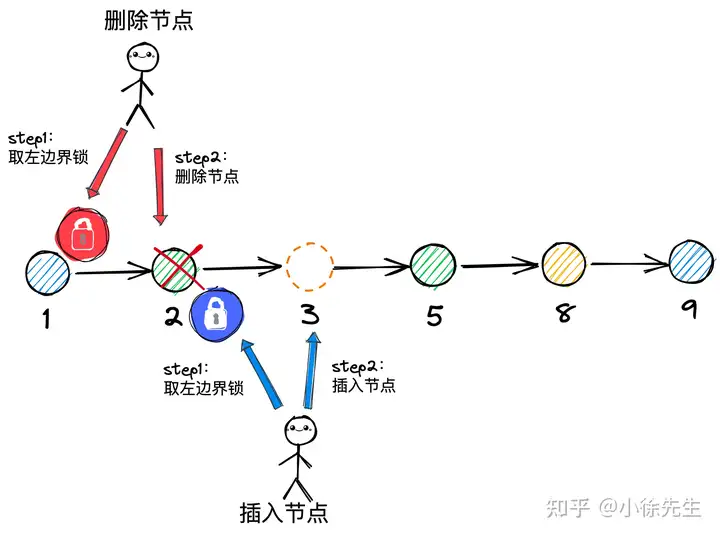
以上图为例,倘若并发执行删除 {key:2},以及插入 {key:3} 两个操作:
- 插入 {key:3} 的操作首先会对 {key:2} 节点加写锁,然后再调整 {key:2} 的 next 指针,实现 {key:3} 的插入效果
- 删除 {key:2} 的操作可以绕开 {key:2},只需要调整 {key:1} 的 next 指针即可实现删除效果,这样一通操作下来,最终插入的 {key:3} 可能和 {key:2} 一起被误删除,得到的结果示意如下图所示.
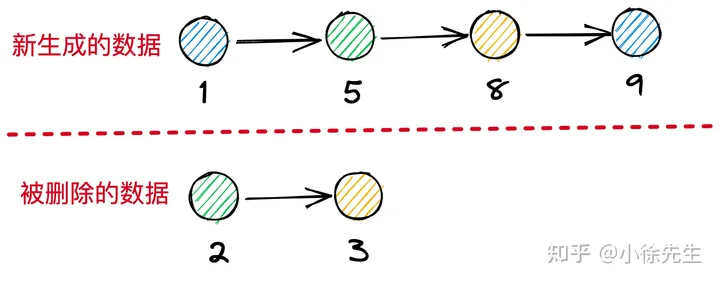
到这里为止,我们需要思考的问题是,在执行删除操作前,应该持有什么范围的锁,才能避免上面这种 bad case 的出现呢?
首先,光是使用左边界锁模型肯定不够,比如上例当中,我们在删除 {key:2} 前先取得左边界 {key:1} 的写锁,但是这并不能避免 {key:2} 之后并发插入的 {key:3} 节点的误删除情况;
其次,倘若我们同时对左边界 {key:1} 和拟删除节点 {key:2} 进行加锁,同时由于加锁时序的问题,倘若尝试插入 {key:3} 的 goroutine 在持有左边界 {key:2} 的写锁时,发现 {key:2} 刚刚已经被删除,则在该层的遍历操作还需要进行回退,这个过程会产生很高的复杂度.
关于并发跳表的 delete 操作,我暂时没有想到很好的处理方式,因此在这里先偷懒了,将 delete 操作和 put、get 进行隔离,退化成全局互斥串行的模型,如果大家有更好的想法,欢迎交流讨论.
2.4 ceiling
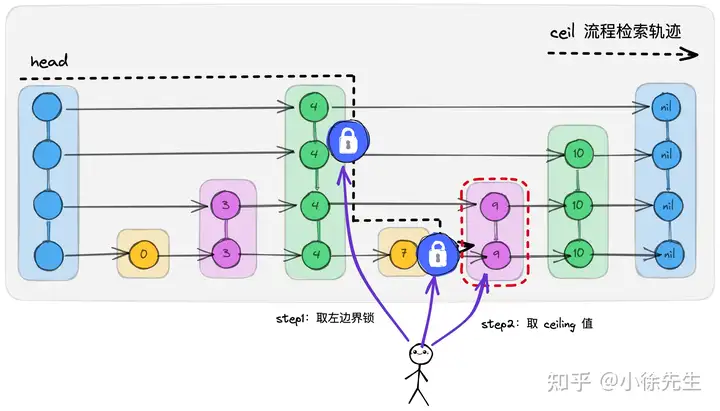
ceiling 操作指的是基于 target 寻找到 key 大于等于 target 且最接近 target 的 key-value 对.
ceiling 操作是适用于左边界锁模型的,通过其检索轨迹可以看出,它需要找到的目标也是左边界右侧的第一个节点,因此其处理流程和 get 操作类似,逐层检索遍历,依次对左边界加读锁,直到找到目标节点后返回结果.
2.5 floor
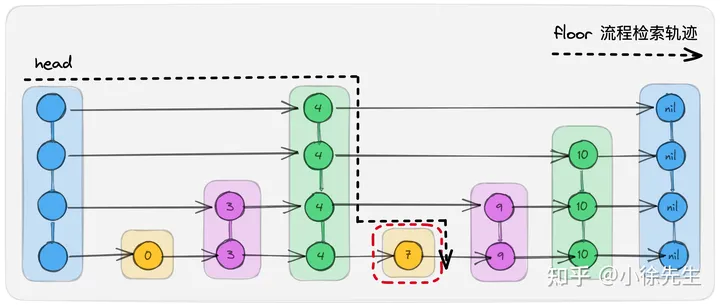
floor 操作指的是基于 target 寻找到 key 小于等于 target 且最接近 target 的 key-value 对.
根据 floor 检索轨迹可以看出,它要寻找的目标节点并不是左边界右侧的第一个节点,这个目标 node 可能位于左边界的左侧,因此仅通过左边界锁未必能保证目标 node 的并发安全性.
综上,floor 操作不适用于左边界锁模型,需要和 put 操作互斥,但是本身属于读操作,因此和 get 操作又可以共享.
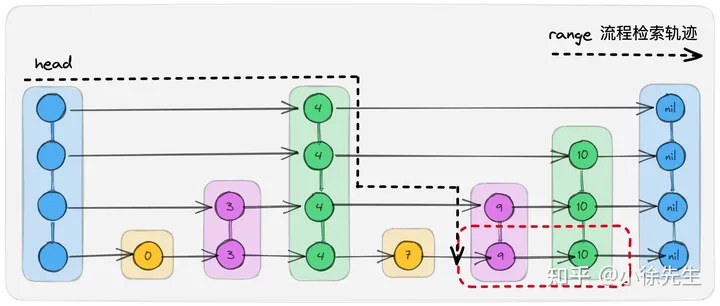
2.6 range
range 操作也同样不适用于左边界锁模型,因为其涉及到的 node 对象可能有多个,没办法被左边界锁模型所完整覆盖到. 和 floor 相类似,range 和 put 操作互斥,但是本身属于读操作,因此和 get 操作又可以共享.
3 落实到代码
下面进入源码展示环节,其中核心方法只包含 get、put 和 delete,几个进阶 API: ceiling、floor、range 暂时没有涉及.
3.1 几类锁

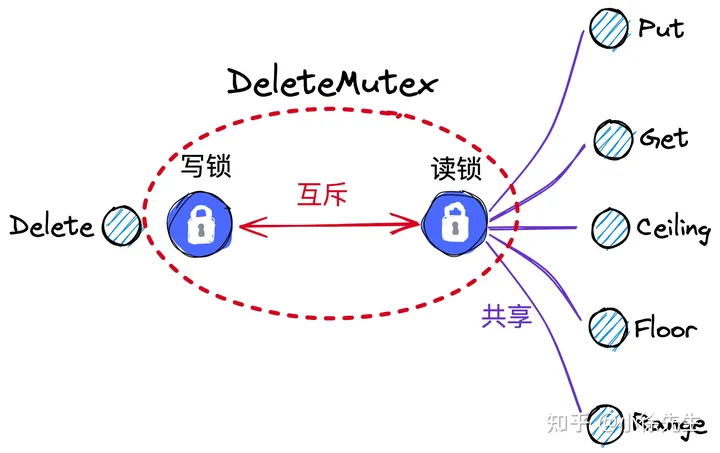
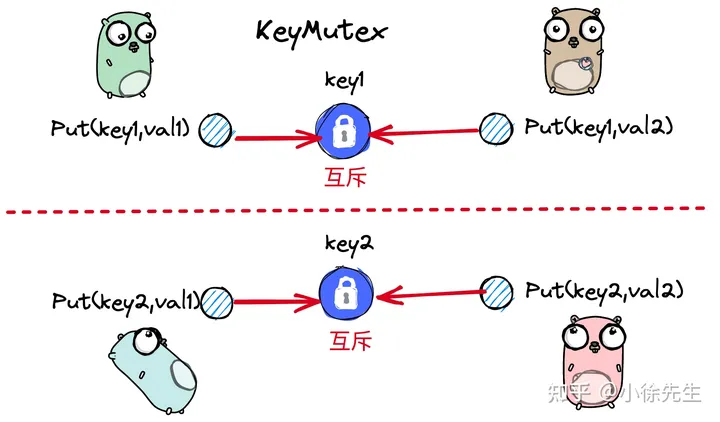
ConcurrentSkipList 中涉及到三类锁:
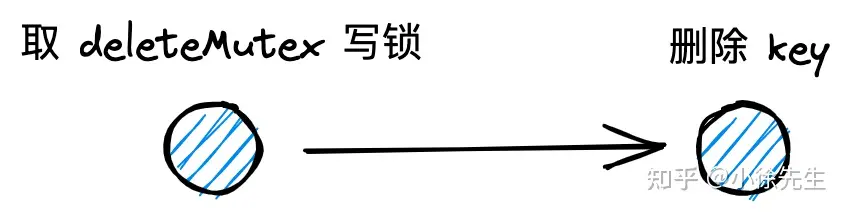
- deleteMutex:一把全局的读写锁;get、put 操作取读锁,实现共享;delete 操作取写锁,实现全局互斥
- keyMutex:每个 key 对应的一把互斥锁. 针对同一个 key 的 put 操作需要取 key 锁实现互斥
- nodeMutex:每个 node 对应的一把读写锁. 在 get 检索过程中,会逐层对左边界节点加读锁;put 在插入新节点过程中,会逐层对左边界节点加写锁.
3.2 delete
3.3 get
3.4 put
4 总结
本篇和大家探讨的问题是,如何基于细粒度锁实现一个并发安全的跳表结构. 细粒度锁主要基于左边界节点锁模型实现.
本文存在几点局限如下:
- 跳表的 delete 操作没有基于细粒度锁实现,而是退化为全局锁
- 存在几个不适用于左边界锁模型的操作,如 range、floor 操作,对应的解决方案没有讨论到
- 并发跳表 ConcurrentSkipList 的实现是我个人闭门造车的产物,第 3 节实现代码中可能存在 bug,并且缺少性能测试作为支撑
针对以上几点,下期会出一篇主题为 bugfix 以及性能压测的文章,对本期的内容加以完善. 也欢迎大家在此期间对本篇内容不周到之处进行批评指正,对于有命中到问题关键点的意见,我也会在下篇内容中予以体现.